Introduction
The surface area of a cube is the sum of the areas of its faces. It is the measurement of the entire outside of a three-dimensional object, and it can be used to determine the total amount of material needed to construct the object. Understanding how to calculate the surface area of a cube is important for a variety of tasks, from construction to engineering calculations.
Step-by-Step Guide to Calculating the Surface Area of a Cube
Calculating the surface area of a cube requires knowledge of the dimensions of the cube. The first step is to identify the length, width, and height of the cube. Once these values are known, they must be multiplied together to obtain the surface area of the cube. This can be done using the following formula:
Surface area = Length x Width x Height
In addition to this formula, there are other formulas that can be used to calculate the surface area of different shapes. These include formulas for cylinders, pyramids, cones, and spheres.
An Easy Formula for Finding the Surface Area of a Cube
The easiest formula for measuring the surface area of a cube is 6 times the length of one side. This formula is based on the fact that a cube has six equal sides, each of which has the same area. To use this formula, simply multiply the length of one side by 6 to obtain the surface area of the cube.
For example, if the length of one side of a cube is 5 cm, then the surface area of the cube is 30 cm² (5 cm x 6).
How to Use Geometry to Find the Surface Area of a Cube
Geometry can also be used to calculate the surface area of a cube. To do so, begin by identifying the faces of the cube. A cube has six faces, all of which are equal in size. Next, explain the relationship between edges and faces. Each edge of the cube connects two faces, and the number of edges is equal to the number of faces.
Once the number of faces and edges has been determined, the area of each face can be calculated. To do so, simply multiply the length of one side by itself. For example, if the length of one side is 5 cm, then the area of one face is 25 cm² (5 cm x 5 cm). Finally, add up the areas of all six faces to obtain the total surface area of the cube.
Explaining the Relationship Between Edges and Faces to Determine the Surface Area of a Cube
The relationship between edges and faces is key to understanding how to calculate the surface area of a cube. A cube has six faces, each of which is connected to four edges. The number of edges is equal to the number of faces, so the cube has a total of 24 edges. By multiplying the length of one side of the cube by itself, the area of one face can be determined. Then, when the areas of all six faces are added up, the total surface area of the cube can be calculated.
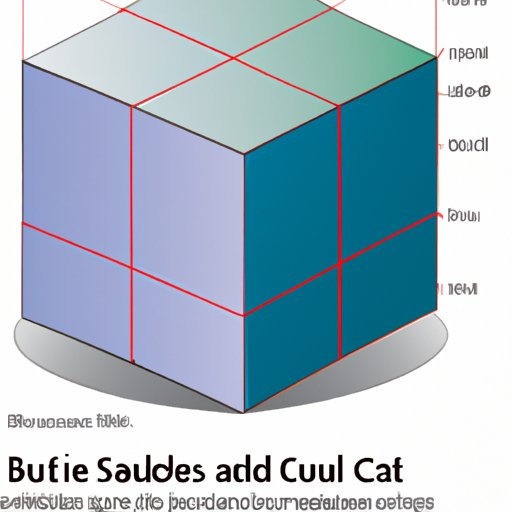
A Visual Guide to Finding the Surface Area of a Cube
A visual guide can be helpful in understanding how to calculate the surface area of a cube. The image below shows the relationship between edges and faces, and how to calculate the area of each face. By adding up the areas of all six faces, the total surface area of the cube can be determined.

A Comprehensive Overview of Calculating the Surface Area of a Cube
To summarize, calculating the surface area of a cube requires knowledge of its dimensions. The first step is to identify the length, width, and height of the cube. Then, the surface area can be calculated using the formula:
Surface area = Length x Width x Height
Alternatively, the surface area can be found by using the easy formula 6 times the length of one side. Additionally, geometry can be used to calculate the surface area of a cube by identifying the faces, explaining the relationship between edges and faces, and calculating the area of each face.
Conclusion
In conclusion, this article has provided a comprehensive overview of calculating the surface area of a cube. It included a step-by-step guide, an easy formula, how to use geometry to calculate surface area, and a visual guide. By following these steps and understanding the relationships between edges and faces, anyone can easily calculate the surface area of a cube.
(Note: Is this article not meeting your expectations? Do you have knowledge or insights to share? Unlock new opportunities and expand your reach by joining our authors team. Click Registration to join us and share your expertise with our readers.)